The Five Stelae of System 7

The Five Stelae of System 7 is on display at the entrance of the Priestley Building.
This artwork presents 5 objects – the “Stelae” – which are engraved with markings which encode a non-periodic sevenfold tiling system.
The artwork evokes both ancient tablets and the space age "Pioneer Plaque". Stelae were made to publish laws and decrees, to record a ruler's exploits and honours, to mark sacred territories or to commemorate military victories. They were widely used in the ancient Near East, Mediterranean, Asia and South America. The Pioneer plaques are a pair of gold-anodized aluminum plaques that were placed on board the 1972 Pioneer 10 and 1973 Pioneer 11 spacecraft, featuring a pictorial message, in the event that either Pioneer 10 or 11 should be intercepted by intelligent extra-terrestrial life.
The Five Stelae correspond to 5 prototiles which form a substitution tiling system. In geometry, a tile substitution is a method for constructing highly ordered tilings. Most importantly, some tile substitutions generate aperiodic tilings - tilings whose prototiles do not admit any tiling with translational symmetry. In this tiling, each tile can be substituted by an arrangement of the other 5 tiles, an iterative procedure which generates increasingly fractal versions of itself. The Five Stelae are an overlay of 3 stages of substitution. This allows the substitution relationships to be understood visually, at once, without needing to see the process.The hieroglyphs both form the pattern and are generated from the pattern.
The 5 hieroglyphs correspond to the 5 tiles used in the tiling. Each stroke of the markings originates in a location of 7-fold rotational symmetry in the next-highest order of the substitution process. Visually, this creates a "join the dots" effect in the hieroglyphs, which "explains" the lines and makes them more than just a random design. However, the meaning is purely self-referential, this self-referential system communicates the wonder of mathematics, which is an abstract system which works due to its perfect system of rules, which are in many ways meaningless, and yet feel mystical in their perfection.
In the words of the artist Richard Hassell "mathematics has a strange, beautiful, abstract wonder and even a kind of cosmic alien horror: a set of knowledge created by humans, but that seems to exist outside of any natural domain. Like something found from an unknown civilization, this art piece presents mathematics to the viewer as something both ancient and futuristic, as something encoded and abstract, as something difficult and complex but also ordered and beautiful."
Tiling
A tiling is a way to fill a 2-dimensional space using repeated copies of a small number of basic pieces, called prototiles. Think of an infinite chessboard (where the prototile is a square), or the honeycomb in a beehive (where the prototile is a hexagon).
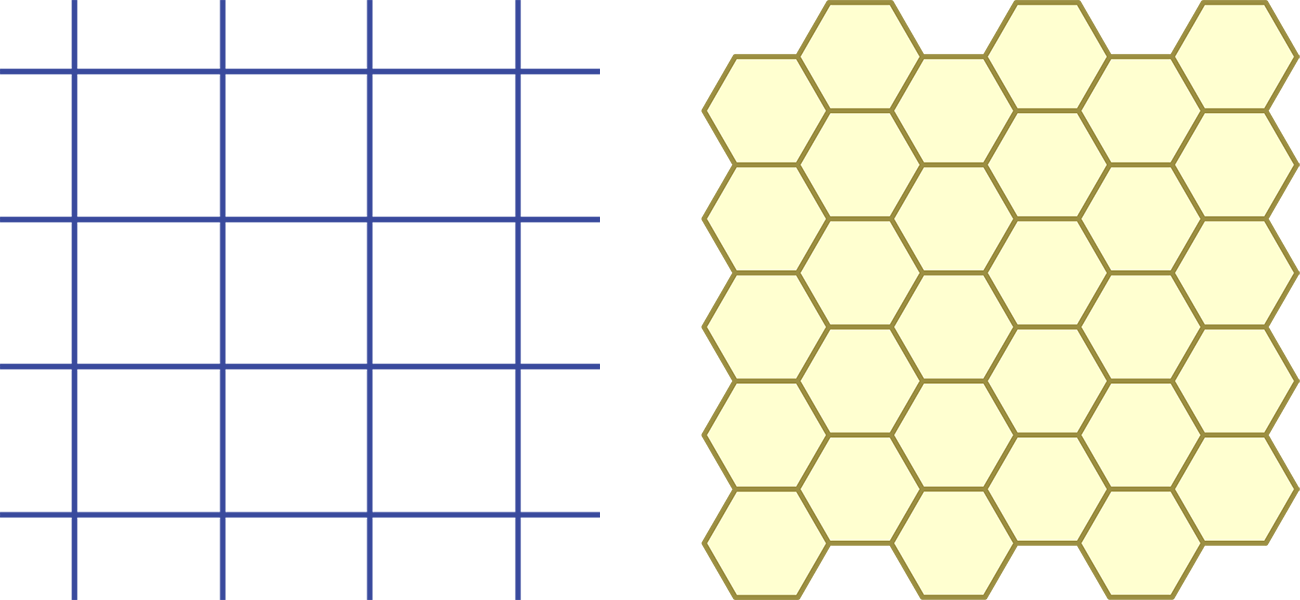
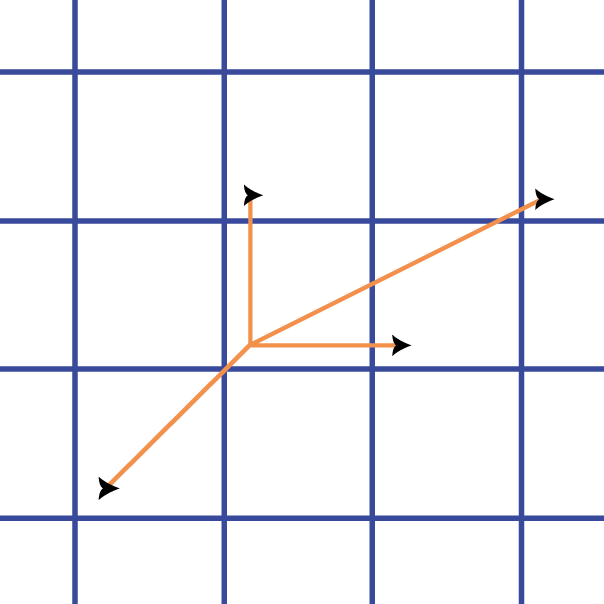
Many common tilings are periodic: you can translate (i.e., shift) the tiling, without rotating or resizing the tiles, to obtain exactly the same picture. For example, the infinite chessboard can be translated horizontally, or vertically, or along any rational slope (a diagonal whose gradient is a fraction p/q).
In contrast, this artwork exhibits an aperiodic set of prototiles. These 5 prototiles – the “five stelae” of the artwork – together tile the plane through infinite repetition. However, it is impossible to combine them in a way that exhibits a translational symmetry as described above.
Instead, the symmetries of this tiling are fractal: each prototile can be built from smaller copies of the 5 prototiles. These in turn can be built from even smaller copies, and so on, ad infinitum. Likewise, you can combine the prototiles to form increasingly larger copies of these prototiles, offering endless possibilities to expand the tiling further and further outwards, towards infinity.
You can see this fractal structure directly on the artwork. Each of the 5 prototiles is represented by a simple hieroglyph. If you look closely, you can see these hieroglyphs repeated at different scales, showing 3 layers of the construction at increasingly smaller scales.

As well as this fractal structure, you can see an interplay between symmetries of the individual prototiles. Look out for symmetries through reflection and rotation, including a rare 7-fold rotational symmetry.
There are other examples of fractal tilings to be found – for example, if you are ever in Naarm/Melbourne then you can stop by Federation Square to see the Conway-Radin pinwheel tiling on the side of one of the buildings.

The pinwheel tiling is simpler than the tiling you see here on the Priestley Building: it uses a single triangular prototile, build from 5 smaller copies of itself. As you explore the fractal structure you can see copies of this triangle rotated to point in infinitely many different directions.

Want to learn more about the mathematics of tilings? Check out The Tiling Book by Colin Adams, which is available electronically through the UQ Library.
